Эконометрика

Список вопросов

1. Классификация переменных в эконометрических моделях.
2. Понятие идентифицируемости модели.
3. Парная регрессия и понятие корреляции.
4. Обобщенная линейная модель множественной регрессии.
5. Нелинейные модели регрессии и их линеаризация.
6. Структурная и приведенная формы системы эконометрических уравнений.
7. Разновидности метода наименьших квадратов.
8. Компоненты временного ряда, аддитивная и мультипликативная модели.

Классификация переменных в эконометрических моделях.

Эконометрика — это раздел экономики, занимающийся разработкой и применением статистических методов для измерений взаимосвязей между экономическими переменными.
Эконометрические модели – это формализованное описание различных экономических явлений и процессов.

Виды эконочметрических моделей:

• парная регрессия (устанавливает зависимость между двумя переменными);
• множественная регрессия (переменная зависит от двух или более факторов);
• система экономических уравнений (факторы от которых зависит переменная требуют не одного, а нескольких уравнений);
• модели временных рядов (значение переменной за ряд последовательных моментов времени).

Экономические переменные, участвующие в любой эконометрической модели (например y=f(x)), делятся на четыре вида:

• экзогенные (независимые) — переменные, значения которых задаются извне. В определенной степени данные переменные являются управляемыми (x);
  
  
• эндогенные (зависимые) — переменные, значения которых определяются внутри модели, или взаимозависимые (y);
  
  
• лаговые — экзогенные или эндогенные переменные в эконометрической модели, относящиеся к предыдущим моментам времени и находящиеся в уравнении с переменными, относящимися к текущему моменту времени. Например, xi-1 — лаговая экзогенная переменная, yi-1 — лаговая эндогенная переменная;
  
  
• предопределенные (объясняющие переменные) — лаговые (xi-1) и текущие (x) экзогенные переменные, а также лаговые эндогенные переменные (yi-1).

Понятие идентифицируемости модели.

Идентификация – это соответствия между приведенной и структурной формами модели.
Приведенная форма модели – каждое уравнение представляет собой решение системы уравнений модели, заданной в структурной форме.
Структурная форма модели – модель записана в виде системы уравнений.

• Модель идентифицируема – если все ее структурные коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, то есть если число параметров структурной формы модели равно числу параметров приведенной формы модели.
  
  
• Модель неидентифицируема – если число структурных коэффициентов больше числа приведенных коэффициентов и следовательно, структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели.
  
  
• Модель сверхидентифицируема, если число приведённых коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведённой формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведённой формы.

Сверхидентифицируемая модель в отличие от неидентифицируемой модели практически решаема, но требует для этого специальных методов исчисления параметров. Система считается идентифицированной, если все уравнения идентифицируемы. Если хоть одно уравнение сверхидентифицируемо, то вся система считается сверхидентифицируемой. Если хоть одно из уравнений системы неидентифицируемо, то считается, что вся система неиндетифицируема.

Парная регрессия и понятие корреляции.

Парная регрессия– представляет собой зависимость между двумя переменными x и y, т.е. y=f(x), где y – зависимая переменная, x – независимая переменная.
Парная линейная регрессия – линейная связь между двумя переменными x и y (описывается в виде прямой), уровнение y = a + bx, где b – коэффициент регрессии, a – свободный член уравнения регрессии.
Парная нелинейная регрессия – нелинейная связь между двумя переменными x и y (описывается в виде кривой, для описания используют логарифмические, экспоненциальные или степенные функции), уравнение y = a + b ln(x). Чем ближе точки к графику, тем теснее связь между переменными.
Корреляция — взаимосвязь двух или нескольких случайных величин. При этом изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой корреляции двух случайных величин служит коэффициент корреляции.
Коэффициент корреляции – это показатель характера взаимного влияния изменения двух случайных величин. Обозначается буквой R и принимает значение от -1 до +1. Если значение по модулю находится ближе к 1 – это означает наличие сильной связи, а если ближе к 0 – связь слабая или вообще отсутствует. Коэффициент корреляция может быть положительным и отрицательным. Отрицательная корреляция – увеличение одной переменной связано с уменьшением другой переменной. Положительная корреляция – увеличение одной переменной связано с увеличением другой переменной.
Дисперсия – это отклонение значений случайной величины относительно среднего значения.
Коэффициент детерминации – наиболее эффективная оценка адекватности регрессионной модели.

Обобщенная линейная модель множественной регрессии.

Модель множественной регрессии – решает задачу зависимости одной зависимой переменной (Y) от нескольких объясняющих переменных (X1, X2,…, Xn). Уравнение модели: Yi=f(Xi1, Xi2, …, Xin). Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а так же совокупное воздействие факторов на моделируемый показатель. Построение модели множественной регрессии начинают с решения вопроса о спецификации модели, который включает 2 этапа:

• отбор факторов;
• выбор вида уравнений регрессии.

Индекс множественной корреляции – оценивает тесноту связи по всей совокупности факторов.
Индекс множественной детерминации – оценивает качество подбора уравнений регрессии.
В обобщенной модели дисперсии объясняющих переменных могут быть произвольными.

Нелинейные модели регрессии и их линеаризация.

Регрессии нелинейные по объясняющим переменным, но линейные по оценивающим параметрам – для расчета параметров нелинейной регрессии применяется метод наименьших квадратов, после предварительной процедуры линеаризации функции регрессии. Приводятся к линейным путем замены переменных. Нелинейная регрессия y = a + b*ln(x) приводится к линейной y = a + bx', где x' = ln(x).
Регрессии нелинейные по оценивающим параметрам:

• нелинейные модели внутри линейных (приводятся к линейному виду);
• нелинейные модели внутри нелинейных.

Для оценки параметров нелинейной модели используется два подхода:

• линеаризация модели (с помощью преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения);
• методы нелинейной оптимизации (применяются когда подобрать линеаризирующее преобразование не получается).

Структурная и приведенная формы системы эконометрических уравнений.

Факторы, от которых зависит переменная требуют не одного уравнения, а нескольких. Таким образом составляется системы эконометрических уравнений.
Структурная форма подразумевает наличие нескольких уравнений и функций в модели.
Приведенная форма – это уравнение, являющееся решение системы уравнений в структурной форме.

Разновидности метода наименьших квадратов.

Суть метода наименьших квадратов заключается в выборе такой линии регрессии, чтобы сумма квадратов отклонений по вертикали между точками и этой линией была бы минимальной.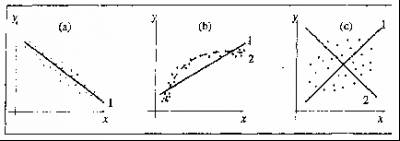


Разновидности методов:

• Обычный метод наименьших квадратов.
• Нелинейный метод наименьших квадратов.
• Косвенный метод наименьших квадратов.
• Взвешенный метод наименьших квадратов.
• Трехшаговый метод наименьших квадратов.

Компоненты временного ряда, аддитивная и мультипликативная модели.

Временной ряд – это последовательность наблюдений некоторой величины в последовательные моменты времени. Отдельные наблюдения называются уровнями ряда (Yt), где t число уровней. Составляющие временного ряда Yt=Ut+Vt+Ct+Et:

• Ut – трэнд, плавно меняющаяся компонента, описывает длительное изменение величины;
• Vt – сезонная компонента, повторяемость экономических процессов в течении не очень долгого периода времени (месяц, год);
• Ct – циклическая компонента, повторяемость экономических процессов в течении длительного периода времени;
• Et – случайная компонента, отражающая влияние не поддающихся учету случайных факторов.

Аддитивные модели представляют собой обобщение множественной регрессии (которая является частным случаем общей линейной модели). Используют операцию сложения (Y=X1+X2+X3).
Мультипликативные модели используют операцию умножения (Y=X1*X2*X3).